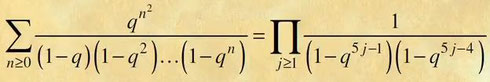Constante de Kaprekar pour les nombres à trois chiffres
F.Quet - Démonstration de la constante de Kaprekar pour les nombres à quatre chiffres
Démonstration de la propriété d’Euler sur le rapport entre produit de nombres pairs et produit de nombres impairs
Démonstration du fameux quotient de 1 par 998 001
Proposition de démonstration très incomplète de cette magnifique formule de mathématique de Ramanujan.pdf
Ci-dessous, d'autres formules de Ramanujan
Voici une des belles formules découverte en 1910 par Ramanujan
qui permet de calculer 8 décimales de Pi à chaque itération
En 1994, David Chudnovsky et les frères Gregory dépassent Ramanujan
en proposant une formule fournissant 14 décimales à chaque itération
